Hybrik Sources - asset_complex
The asset_complex allows you to combine elements from multiple source files containing video, audio, and/or text components into a single logical source. It also allows you to stitch multiple sources together in a sequence with the ability to trim each source, allowing for advanced editing operations. Depending on what you are trying to do, the structure will differ slightly but the base structure will look like this:
* asset_complex
* asset_version[0]
* asset_component[0]
* asset_component[1]
* asset_version[1]
* asset_component[0]
...
The asset_complex is comprised of one or more asset_versions, each of which are comprises one or more asset_components. Each asset_version represents an individual clip in the sequence, each of which could consist of video, audio, and/or text tracks. Each asset_component defines a source file that provides these audio, video, or text tracks in the asset_version.
Sequence
In the asset_complex, each asset_version is stitched together into a sequence.
{
"uid": "my_asset_complex",
"kind": "source",
"payload": {
"kind": "asset_complex",
"payload": {
"kind": "sequence",
"asset_versions": [
{
"version_uid": "first_in_sequence",
"asset_components": [
{
"component_uid": "audio_and_video",
"kind": "name",
"name": "source_file_one.mov"
}
]
},
{
"version_uid": "second_in_sequence",
"asset_components": [
{
"component_uid": "audio_and_video",
"kind": "name",
"name": "source_file_two.mov"
}
]
}
]
}
}
},
In the above example, the payload kind of our source is of type asset_complex. The asset_complex has a payload with a sequence. Let’s take a look at how these two assets are being put together in the Source Pipeline which the rest of the job uses.
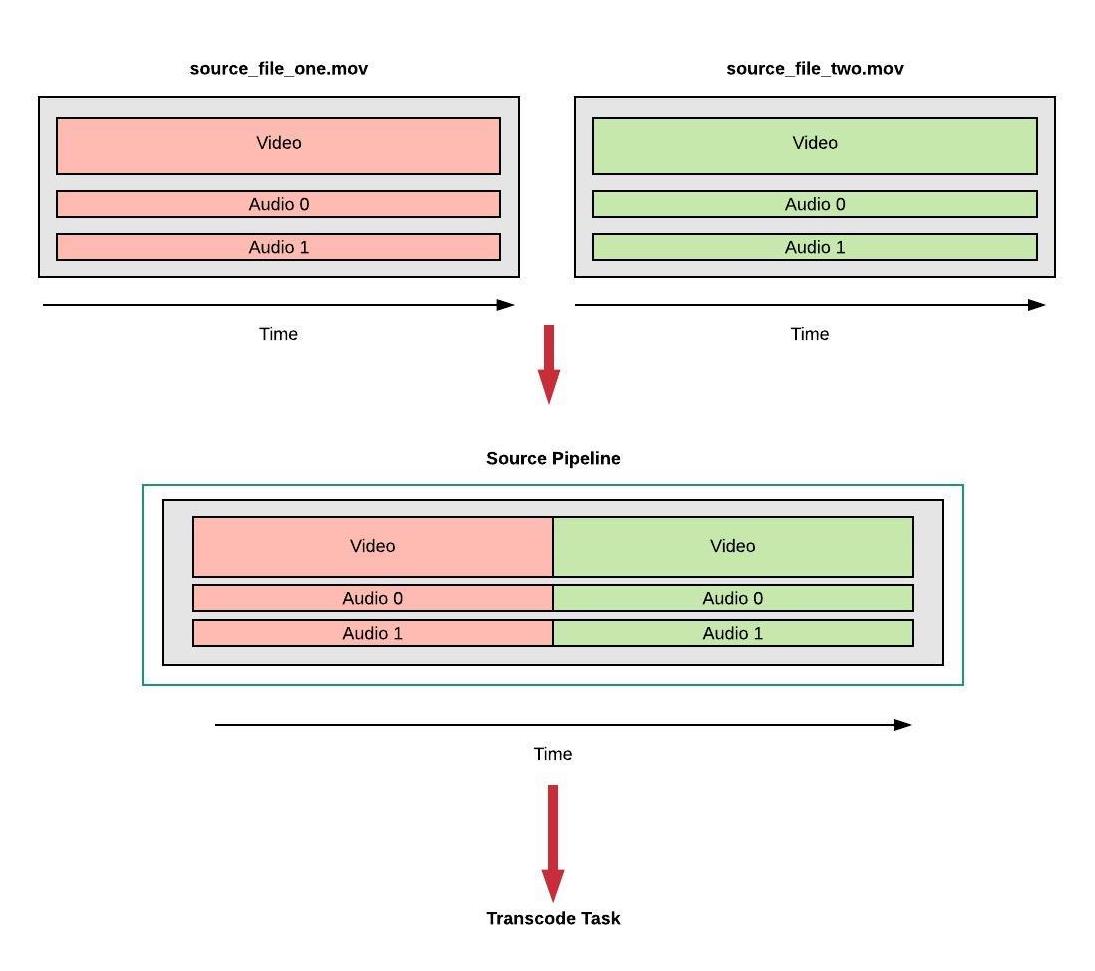
A More Complex Sequence
Sometimes you might want to use audio from one source and video from another. This could include mapping audio tracks or trimming sources.
Here is an example where our first clip uses audio and video from a single file, followed by a second clip with audio from a third file. Conceptually our sequence will look like this:
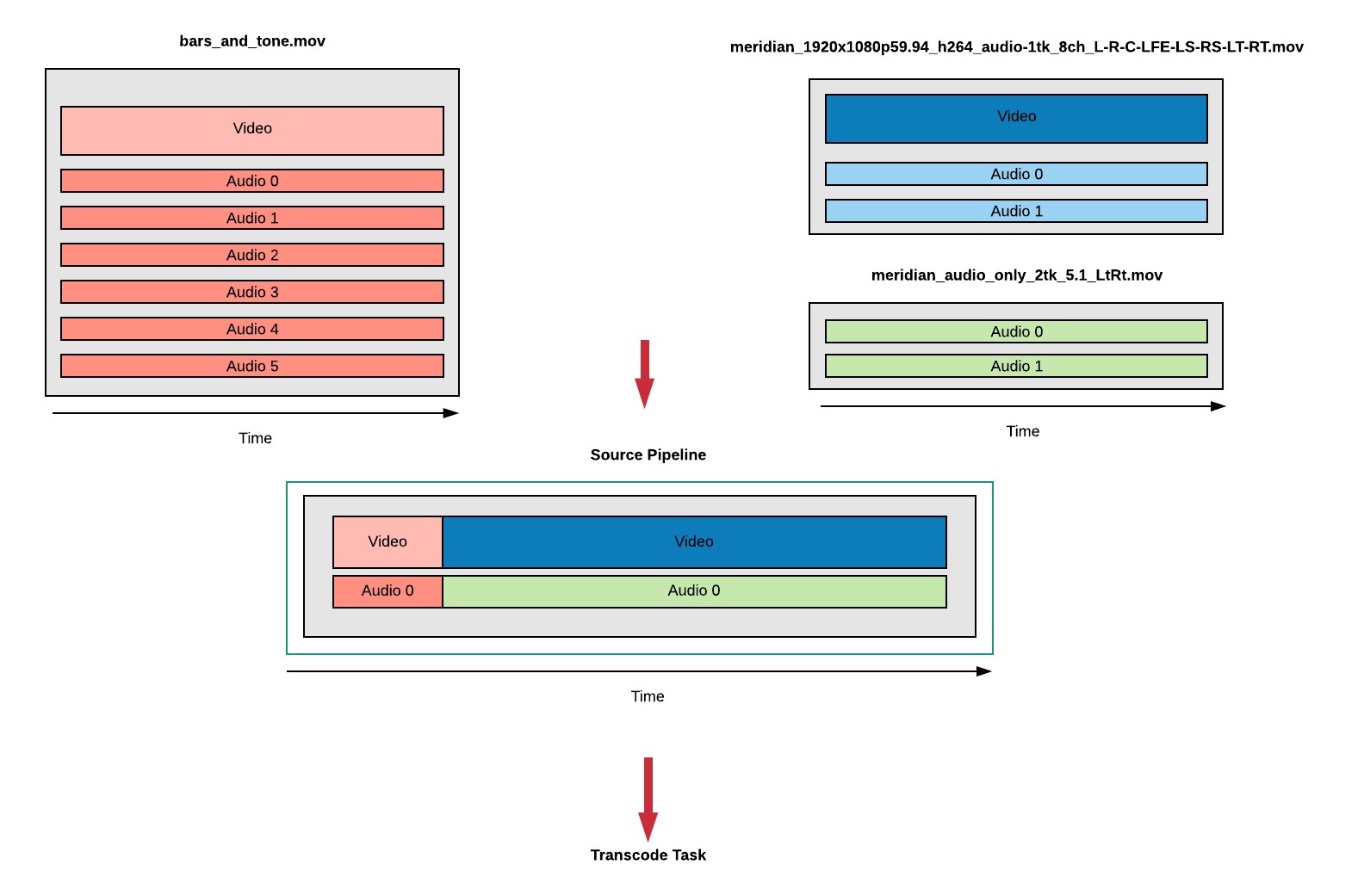
Here is the matching json which trims our bars and tone, maps the audio and then stitches our second clip and audio track together.
{
"uid": "sources",
"kind": "source",
"payload": {
"kind": "asset_complex",
"payload": {
"kind": "sequence",
"asset_versions": [
{
"version_uid": "first_in_sequence",
"asset_components": [
{
"kind": "name",
"name": "bars_and_tone.mov",
"location": {
"storage_provider": "s3",
"path": "{{source_path}}"
},
"contents": [
{
"kind": "video"
},
{
"kind": "audio",
"map": [
{
"input": {
"track": 0,
"channel": 0
},
"output": {
"track": 0,
"channel": 0
}
}
]
}
],
"trim": {
"inpoint_sec": 0,
"outpoint_sec": 30
}
}
]
},
{
"version_uid": "second_in_sequence",
"asset_components": [
{
"kind": "name",
"name": "meridian_1920x1080p59.94_h264_audio-1tk_8ch_L-R-C-LFE-LS-RS-LT-RT.mov",
"location": {
"storage_provider": "s3",
"path": "{{source_path}}"
},
"contents": [
{
"kind": "video"
}
]
},
{
"kind": "name",
"name": "meridian_audio_only_2tk_5.1_LtRt.mov",
"location": {
"storage_provider": "s3",
"path": "{{source_path}}"
},
"contents": [
{
"kind": "audio",
"map": [
{
"input": {
"track": 0,
"channel": 0
},
"output": {
"track": 0,
"channel": 0
}
}
]
}
]
}
]
}
]
}
}
},
Read more on mapping, trimming, and the contents array in our other tutorials:
An Image Sequence as a Source
If you had an asset that consisted of thousands of .png files, called animation0001.png, animation0002.png, … animationN.png, etc. that you wanted to transcode into a single output, you could specify it in this way. You can manually specify a frame_rate for your source:
{
"uid": "source_file",
"kind": "source",
"payload": {
"kind": "asset_complex",
"payload": {
"asset_versions": [
{
"location": {
"storage_provider": "s3",
"path": "{{source_path}}"
},
"asset_components": [
{
"kind": "image_sequence",
"image_sequence": {
"base": "animation%04d.png",
"frame_rate": 24
}
}
]
}
]
}
}
}
Multiple Elements Not in a Sequence
If you wanted to pass several existing assets from a source task to a package task, you can do so with an asset_complex with a type of multi.
{
"uid": "source_files",
"kind": "source",
"payload": {
"kind": "asset_complex",
"payload": {
"kind": "multi",
"location": {
"storage_provider": "s3",
"path": "{{source_path}}"
},
"asset_versions": [
{
"version_uid": "v",
"asset_components": [
{
"kind": "name",
"name": "video_layer1.ts",
},
{
"kind": "name",
"name": "audio_english.ts",
"language": "eng"
}
]
}
]
}
}
},
IMF as a source
IMF, or Interoperable Master Format, is a set of SMPTE standards for describing assets that make up a piece of content, as well as how those pieces of content should be assembled for delivering to specific markets (foreign countries, airline playback, etc). This eliminates the need to maintain masters for each market. The IMF contains video, audio, and data essences, as well as Composition Playlists (CPLs) for each deliverable that describe how to assemble the essences into a fully composed output. Composition Playlists can be thought of similarly to sequences or Edit Decision Lists (EDLs) that are generated by video editing software.
{
"uid": "source_file",
"kind": "source",
"payload": {
"kind": "asset_url",
"payload": {
"storage_provider": "s3",
"url": "{{source_path}}/imf/source_cpl.xml",
"options": {
"resolve_manifest": true
}
}
}
},
Under the hood, the source is converted into an asset_complex. Because of this, here are a few restrictions with this kind of source.
- If you have a CPL as a source, no other sources may be added (eg, no additional
asset_versions). If you need to stitch bumpers, you can update your CPL or first render the CPL to a mezzanine format and then build anasset_complex. - You cannot remap audio in the source, however you can remap audio in the target.
- You may have one trim on the CPL. If your CPL’s media is all the same frame rate, you may trim by any trim operation. If the media has mixed frame rates, only trimming by seconds will be valid (
duration_sec,inpoint_sec, oroutpoint_sec). - Segmented Rendering has limited support and may be buggy.
- If the CPL is “simple”, meaning having no edits in the component tracks,
segmented_renderingmay be supported - If the CPL is “complex”, having edits,
segmented_renderingis not supported.
Folder Enum Source
Let’s say that you want to run the same operation in a job over a series of source files. The folder_enum source kind will do just that. You can input a path and a wildcard pattern to match filenames. Using a * wildcard will match all files in a your source path directory. If you wanted to match all mp4 files for example, you could use *.mp4. For each file matching the pattern, a new copy of the job will be spawned. The folder_enum source looks like this:
{
"uid": "folder_enum",
"kind": "folder_enum",
"task": {
"retry_method": "retry",
"retry": {
"count": 2,
"delay_sec": 30
}
},
"payload": {
"source": {
"storage_provider": "s3",
"path": "{{source_path}}"
},
"settings": {
"pattern_matching": "wildcard",
"wildcard": "*",
"recursive": true
}
}
},
The recursive option takes a boolean and will recursively search for files in subdirectories of the provided source path.
Because the folder_enum source creates copies of the job, it is important to have your target names use {source_basename} so that your outputs do not overwrite each other.
Examples: